(几何证明选讲)如图所示,⊙ 的两条切线
的两条切线 和
和 相交于点
相交于点 ,与⊙
,与⊙ 相切于
相切于 两点,
两点, 是⊙
是⊙ 上的一点,若
上的一点,若 ,则
,则 ________.(用角度表示)
________.(用角度表示)
比较大小: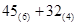
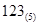
采用系统抽样从含有8000个个体的总体(编号为0000,0001,…,,7999)中抽取一个容量为50的样本,已知最后一个入样编号是7900,则最前面2个入样编号是
某地区为了了解70~80岁老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查.下表是这50位老人日睡眠时间的频率分布表.
| 序号 (I) |
分组 (睡眠时间) |
组中值 (GI) |
频数 (人数) |
频率 (FI) |
| 1 |
[4,5) |
4.5 |
6 |
0.12 |
| 2 |
[5,6) |
5.5 |
10 |
0.20 |
| 3 |
[6,7) |
6.5 |
20 |
0.40 |
| 4 |
[7,8) |
7.5 |
10 |
0.20 |
| 5 |
[8,9] |
8.5 |
4 |
0.08 |
在上述统计数据的分析中,一部分计算见流程图,则输出的S的值是________.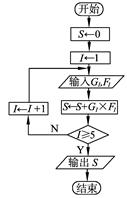
若执行如下图所示的框图,输入x1=1,x2=2,x3=3,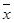 =2,则输出的数等于________.
=2,则输出的数等于________.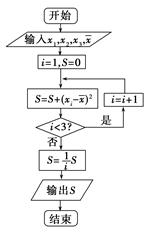
下面是一个算法.如果输出的y的值是20,则输入的x的值是. 