如图所示，在平面直角坐标系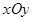
中，矩形OABC的边长OA、OC分别为12cm、6cm，点A、C分别在
轴的负半轴和
轴的正半轴上，抛物线
经过点A、B，且18
+
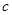=0．
（1）求抛物线的解析式；
（2）如果点P由点A开始沿AB边以1cm/s的速度向终点B移动，同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动．
① 移动开始后第t秒时，设△PBQ的面积为S，试写出S与t之间的函数关系式，并写出t的取值范围；
②当S取得最大值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由．
类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位。用有理数加法表示为3＋（－2）=1。若坐标平面上的点做如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移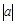
个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移
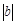个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为
。
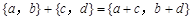解决问题：计算：{3，1}＋{1，－2}；
动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”
{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”
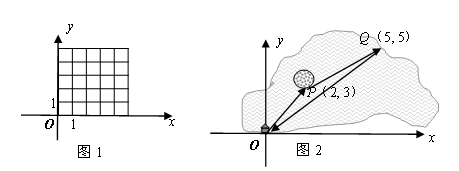
{3，1}平移，最后的位置还是点B吗? 在图1中画出四边形OABC。如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，5），最后回到出发点O. 请用“平移量”加法算式表示它的航行过程。
运输120吨化肥，装载了2节火车皮与5辆汽车；运输220吨化肥，装载了4节火车皮与5辆汽车。求每节火车皮与每辆汽车平均各装多少吨？
如图，已知：DE∥BC，CD是∠ACB的平分线，∠A＝60°，∠ACB＝50°，求∠EDC和∠BDC的度数。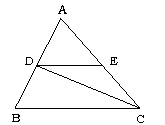
已知△ABC三个顶点的坐标分别是 A（– 3，–1）、B（1，3）、C（2，－3）在平面直角坐标系中描出各点并画出△ABC；
求△ABC的面积。
解方程组
