变化的磁场在其周围空间激发的电场叫涡旋电场,即感生电场.图中虚线为一圆柱状均匀磁场区的横截面,其磁感应强度B随时间均匀变化,感生电场的电场线是涡旋状的同心圆,同一个圆上的各点电场强度大小相等,方向沿圆周的切向.图中实线为其中的一条电场线,半径为r,场强大小为E.若电荷量为+q的粒子沿该电场线逆时针运动一周,电场力做的功为W,忽略粒子运动产生的磁场,则以下说法正确的是( )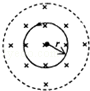
| A.磁感应强度均匀减小,W=0 | B.磁感应强度均匀增大,W=0 |
| C.磁感应强度均匀减小,W=2πqEr | D.磁感应强度均匀增大,W=2πqEr |
有电子、质子、氘核、氚核,以同样速度垂直射入同一匀强磁场中,它们都作匀速圆周运动,则轨道半径最大的粒子是
| A.氘核 | B.氚核 | C.电子 | D.质子 |
下面给出多种用伏安法测电池电动势和内电阻的数据处理方法,其中既减小偶然误差,又直观、简便的方法是
| A.测出两组I,U的数据,代入方程组E=U1+I1r和E=U2+I2r中,即可求出E和r |
| B.多测几组I,U的数据,求出几组E,r,最后分别求出其平均值 |
| C.测出多组I,U的数据,画出U—I图像,再根据图像求E,r |
| D.多测出几组I,U数据,分别求出I和U的平均值,用电压表测出开路时的路端电压即为电压势E,再用闭合电路欧姆定律求出内电阻r |
图5所示电路中,两端电压U恒定,电流表内阻可忽略不计,定值电阻与滑动变阻器的全部电阻相等,均为R,当滑动键P从变阻器的上端C一直移到下端D的过程中,电流表示数情况应是
| A.先减小后增大 | B.先增大后减小 |
| C.恒定不变 | D.始终增大 |
如图4,一带电小球用丝线悬挂在水平方向的匀强电场中,当小球静止后把悬线烧断,则小球在电场中将作
| A.自由落体运动 | B.曲线运动 |
| C.沿着悬线的延长线作匀加速运动 | D.变加速直线运动 |
如图所示,在点电荷-Q的电场中,M,N是两个等势面.现将一点电荷+q,从a点分别经路径①和路径②(经过C点)移到b点,在这两个过程中
| A.都是电场力做功,沿路径①做的功比沿路径②做的功少 |
| B.都是电场力做功,沿路径①做的功等于沿路径②所做的功 |
| C.都是克服电场力做功,沿路径①做的功大于沿路径②做的功 |
| D.都是克服电场力做功,沿路径①做的功等于沿路径②做的功 |