已知函数f(x)的定义域为(﹣∞,+∞),f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(﹣2)=1,f(3)=1,则不等式f(x2﹣6)>1的解集为( )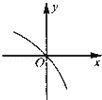
| A.(2,3) |
B.(﹣ , , ) ) |
| C.(2,3)∪(﹣3,﹣2) |
D.(﹣∞,﹣ )∪( )∪( ,+∞) ,+∞) |
班级英语兴趣小组有5名男生5名女生,现在要从中选4名学生参加学校的英语演讲比赛,要求男、女生都有,则不同选法有( )
| A.210种 | B.200种 | C.120种 | D.100种 |
如图所示,按棋盘格子形排列着16个点子,若从中每次选取不在一直线上的3个点,作为一个三角形的顶点,试问一共可作出多少个三角形?
某乒乓球队共有男女队员18人,现从中选出男、女队员各1人组成一对双打组合,由于在男队员中有2人主攻单打项目,不参与双打组合,这样一共有64种组合方式,则乒乓球队中男队员的人数为( )
| A.10人 | B.8人 | C.6人 | D.12人 |
有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选出4人承担这三项任务,不同的选法种数有( )
| A.1 260种 | B.2 025种 | C.2 520种 | D.5 040种 |
从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为( )
| A.56 | B.52 | C.48 | D.40 |