设a1,a2,…,an为正数,求证: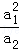 +
+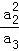 +…+
+…+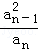 +
+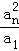 ≥a1+a2+…+an.
≥a1+a2+…+an.
如下图(图1)等腰梯形PBCD,A为PD上一点,且AB⊥PD,AB=BC,AD=2BC,沿着AB折叠使得二面角P-AB-D为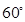 的二面角,连结PC、PD,在AD上取一点E使得3AE=ED,连结PE得到如下图(图2)的一个几何体.
的二面角,连结PC、PD,在AD上取一点E使得3AE=ED,连结PE得到如下图(图2)的一个几何体.
(1)求证:平面PAB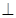 平面PCD;
平面PCD;
(2)求PE与平面PBC所成角的正弦值.
在锐角三角形ABC中,角A,B,C所对的边分别为 ,且
,且
(1)求角A;
(2)若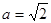 ,求
,求 的取值范围.
的取值范围.
等比数列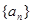 为递增数列,且
为递增数列,且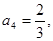
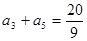 ,数列
,数列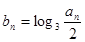 (n∈N※)
(n∈N※)
(1)求数列 的前
的前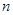 项和
项和 ;
;
(2)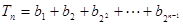 ,求使
,求使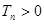 成立的最小值
成立的最小值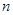 .
.
(本小题满分14分)已知函数
 的图像过点
的图像过点 ,且在该点的切线方程为
,且在该点的切线方程为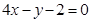 .
.
(Ⅰ)若 在
在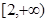 上为单调增函数,求实数
上为单调增函数,求实数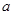 的取值范围;
的取值范围;
(Ⅱ)若函数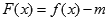 恰好有一个零点,求实数
恰好有一个零点,求实数 的取值范围.
的取值范围.
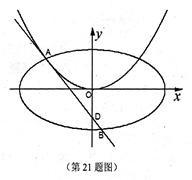
(本小题满分15分)如图,过点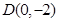 作抛物线
作抛物线 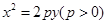 的切线
的切线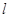 ,切点A在第二象限.
,切点A在第二象限.
(Ⅰ)求切点A的纵坐标;
(Ⅱ)若离心率为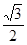
 的椭圆
的椭圆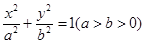 恰好经过切点A,设切线
恰好经过切点A,设切线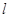 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线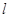 ,OA,OB的斜率分别为
,OA,OB的斜率分别为 ,求椭圆方程.
,求椭圆方程.