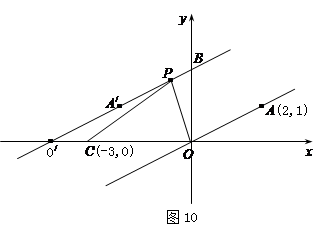(本题10分)已知:抛物线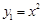 以点C为顶点且过点B,抛物线
以点C为顶点且过点B,抛物线 以点B为顶点且过点C,分别过点B、C作
以点B为顶点且过点C,分别过点B、C作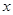 轴的平行线,交抛物线
轴的平行线,交抛物线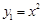 、
、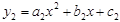 于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.
于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.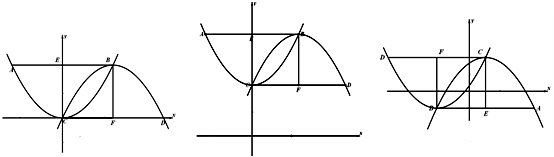
(1)如图1,①求证四边形ECFB为正方形;②求点A的坐标;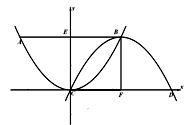
(2)①如图2,若将抛物线“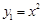 ”改为“
”改为“ ”,其他条件不变,求CD的长;
”,其他条件不变,求CD的长;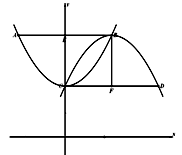
②如图3,若将抛物线“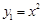 ”改为“
”改为“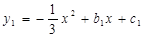 ”,其他条件不变,求
”,其他条件不变,求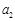 的值;
的值;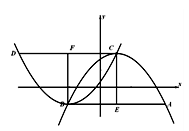
(3)若将抛物线“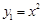 ”改为抛物线“
”改为抛物线“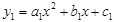 ”,其他条件不变,请用含b2的
”,其他条件不变,请用含b2的
代数式表示b1.
小明与小颖做如下的游戏:用一个均匀的小正方体骰子(每个面分别标有数字1,2,3,4,5,6),现任意掷出小正方体骰子.数字是2的倍数的面朝上的概率是多少?
数字是3的倍数的面朝上的概率是多少?
若规定小正方体骰子抛出后,标着大于数字3的面朝上时,小明获胜;不大于数字3的面朝上时,小颖获胜,这样的游戏公平吗?说说你的理由
已知:如图,在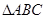 中,
中, 是
是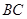 边上的高,
边上的高,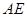 是
是 平分线。求
平分线。求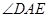 的度数。
的度数。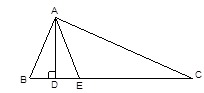
已知, ,
, ,
,
其中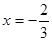 ,
,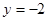 。比较A和B的值的大小。小明说A的值大,
。比较A和B的值的大小。小明说A的值大,
小华说B的值大。请你判断一下,谁的说法正确,为什么?
计算: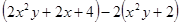


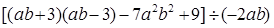
已知正比例函数y=kx经过点A(2,1),如图10所示.求这个正比例函数的关系式.
将这个正比例函数的图像向左平移4个单位,写出在这个平移下,点A、原点O的对应点A/、O/的坐标,求出平移后的直线O/A/所对应的函数关系式.
已知点C的坐标为(-3,0),点P(x,y)为线段O/B上一动点(P与O/、B不重合),设△PCO的面积为S.
①求S与x之间的函数关系式及x的取值范围;
②② 求当S= 时,点P的坐标.
时,点P的坐标.