函数f1（x）＝x3，f2（x）＝
，f3（x）＝
，f4（x）＝
|sin（2πx）|，等差数列{an}中，a1＝0，a2015＝1，bn＝|fk（an＋1）－fk（an）|（k＝1，2，3，4），用Pk表示数列{bn}的前2014项的和，则（ ）
| A．P4＜1＝P1＝P2＜P3＝2 | B．P4＜1＝P1＝P2＜P3＜2 |
| C．P4＝1＝P1＝P2＜P3＝2 | D．P4＜1＝P1＜P2＜P3＝2 |
已知函数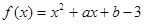
(x∈R) 图象恒过点(2,0)，则a2＋b2的最小值为( )
| A．5 | B． |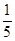
C．4 | D． |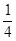
当点M(x，y)在如图所示的三角形ABC内(含边界)运动时，目标函数z＝kx＋y
取得最大值的一个最优解为(1,2)，则实数k的取值范围是( )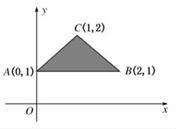
| A．(－∞，－1]∪[1，＋∞) | B．[－1,1] |
| C．(－∞，－1)∪(1，＋∞) | D．(－1,1) |
有编号分别为1，2，3，4，5的5个红球和5个黑球，从中取出4个，则取出
的编号互不相同的概率
为（）
A． |
B． |
C． |
D． |
若A、B为一对对立事件，其概率分别为P(A)＝
，P(B)＝
，则x＋y的最小值为( )
A．9 B．10 C．6D．8
下列结论：
①若命题
；命题
，
则命题“
”是假命题；
②某校在一次月考中约有1000人参加考试，数学考试的成绩
~
，统计结果显示数字考试成绩在70分到110分之间的人数约为总人数的
则此次月考中数学考试成绩不低于110分的学生约有200人；
③在线性回归分析中，残差的平方和越小，说明模型的拟合效果越好；
④对分类变量X与Y，它们的随机变量K2的观测值为k，若k越大，则“X与Y有关
系”的把握程度越大，其中结论正确的个数为（）
| A．4 | B．3 | C．2 | D．1 |