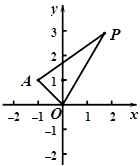
等比数列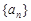 的首项为
的首项为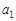 ,公比为
,公比为 ,用
,用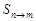 表示这个数列的第n项到第m项共
表示这个数列的第n项到第m项共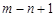 项的和.
项的和.
(Ⅰ)计算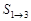 ,
,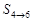 ,
, ,并证明它们仍成等比数列;
,并证明它们仍成等比数列;
(Ⅱ)受上面(Ⅰ)的启发,你能发现更一般的规律吗?写出你发现的一般规律,并证明.
(本小题满分14分)
已知函数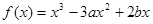 在点
在点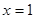 处有极小值-1,
处有极小值-1,
(1)求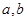 的值(2)求出
的值(2)求出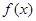 的单调区间.
的单调区间.
(3)求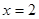 处的切线方程.
处的切线方程.
(本小题满分12分)
已知函数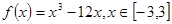 ;
;
(1)求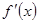 ;(2)求
;(2)求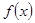 的最大值与最小值.
的最大值与最小值.
(本小题满分12分)
已知复数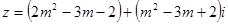 .当实数
.当实数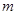 取什么值时,复数
取什么值时,复数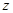 是:
是:
(1)0;(2)虚数(3)复平面内满足 的点对应的复数。
的点对应的复数。
(本小题满分14分)已知 ,函数
,函数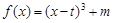 .
.
(Ⅰ)当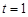 时,
时,
(ⅰ)若 ,求函数
,求函数 的单调区间;
的单调区间;
(ⅱ)若关于 的不等式
的不等式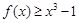 在区间
在区间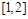 上有解,求
上有解,求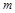 的取值范围;
的取值范围;
(Ⅱ)已知曲线 在其图象上的两点
在其图象上的两点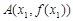 ,
, (
(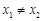 )处的切线分别为
)处的切线分别为 .若直线
.若直线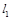 与
与 平行,试探究点
平行,试探究点 与点
与点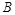 的关系,并证明你的结论.
的关系,并证明你的结论.
(本小题满分12分)在平面直角坐标系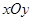 中,已知点
中,已知点
 ,P是动点,且三角形
,P是动点,且三角形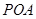 的三边所在直线的斜率满足
的三边所在直线的斜率满足 .
.
(Ⅰ)求点P的轨迹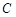 的方程;
的方程;
(Ⅱ)若Q是轨迹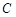 上异于点
上异于点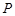 的一个点,且
的一个点,且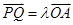 ,直线
,直线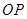 与
与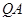 交于点M,试探
交于点M,试探
究:点M的横坐标是否为定值?并说明理由.