如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG。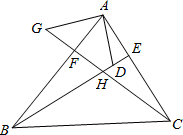
求证：（1）AD=AG，
（2）AD与AG的位置关系如何。
（1）分解因式：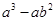
；
（2）先化简，再求值：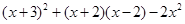
，其中
．
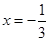图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y（元）与通话时间t（分钟）之间的关系图像．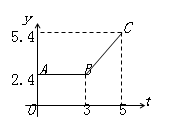
（1）从图像知，通话2分钟需付的电话费是元；
（2）当t≥3时求出该图像的解析式（写出求解过程）；
（3）通话7分钟需付的电话费是多少元？
将长为1，宽为a的长方形纸片
如图左那样折一下，剪下一个边长等于长方形宽度的正方形（称为第一次操作）；再把剩下的长方形如图右那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）．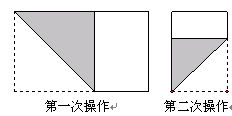
（1）第一次操作后，剩下的长方形的长和宽分别为多少？（用含a的代数式表示）
（2）第二次操作后，剩下的长方形的面积是多少？（列出代数式，不需化简）
（3）假如第二次操作后，剩下的长方形恰好是正方形，则a的值是多少？
如图，直线AE、CF分别被直线EF、AC所截，已知，∠1=∠2，AB平分∠EAC，CD平分∠ACG．将下列证明AB∥CD的过程及理由填写完整．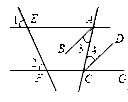
证明：∵ ∠1="∠2" （已知）
∴ AE∥（）
∴ ∠EAC =∠，（ ）
而AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴∠=
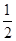∠EAC，∠4=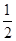∠（角平分线的定义）
∴∠=∠4（等量代换）
∴AB∥CD（）．
小明到商店买东西，下面是他和售货员阿姨的对话：“我买这种牙膏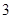
支，这种牙刷
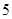把”．“一共
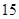元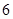
角”．付款后，小明说：“阿姨，这支牙膏我不要了，换一把牙刷吧！”“还需找你
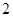元”．从他们的对话中你能知道牙刷、牙膏的单价吗？