十一黄金期间，五台山7天中每天旅游人数的变化情况如下表（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：

日期	1日	2日	3日	4日	5日	6日	7日
人数变化/万人	+0.5	+0.7	+0.8		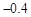	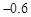+0.2

 
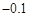（1）请判断7天内游客人数量最多和最少的各是哪一天？它们相差多少万人？
（2）如果9月30日旅游人数为2万人，平均每人消费300元，请问风景区在此7天内总收入为多少万元？

科目 数学   题型 解答题   难度 中等

知识点： 幂的乘方与积的乘方