下列方程中,解是x=4的方程是( )
| A.3x﹣2=10 | B.﹣3x+8=﹣5x | C.x(x﹣1)=﹣4(x﹣1) | D.3(x+2)=3x+2 |
如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )。
AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )。
A、7 B、14 C、17 D、20
在数-1,1,2中任取两个数作为点坐标,那么该点刚好在一次函数 图象上的概率是()。
图象上的概率是()。
A. |
B. |
C. |
D. |
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )。
A. |
B. |
C. |
D. |
据报道,重庆市九龙坡区2013年GDP总量约为770亿元,用科学记数法表示这一数据应为 ()元。
A. 元 元 |
B. 元 元 |
C. 元 元 |
D.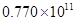 元 元 |
下列计算正确的是()。
A.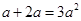 |
B.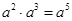 |
C.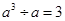 |
D. |