给出以下五个命题:
①命题“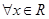 ,
,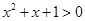 ”的否定是:“
”的否定是:“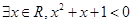 ”.
”.
②已知函数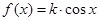 的图象经过点P(
的图象经过点P( ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于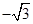
③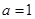 是直线
是直线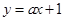 和直线
和直线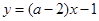 垂直的充要条件.
垂直的充要条件.
④函数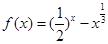 在区间(0,1)上存在零点.
在区间(0,1)上存在零点.
⑤已知向量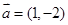 与向量
与向量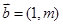 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是( )
)
其中正确命题的序号是 .
用系统抽样的方法从160名学生中抽取容量为20的样本,将160名学生随机地从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,…,153~160号).若第16组抽出的号码为126,则第1组中抽取的号码是_______.
(本小题满分13分)已知椭圆 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合,直线
的焦点重合,直线 :
: 与直线
与直线 :
: 之间的距离为6
之间的距离为6
(Ⅰ)求椭圆 方程;
方程;
(Ⅱ)设椭圆 的左焦点为
的左焦点为 ,
, 与
与 轴的交点为
轴的交点为 ,过点
,过点 作斜率不为零的直线与椭圆
作斜率不为零的直线与椭圆 交于
交于 两点,
两点, 关于
关于 轴对称的点为
轴对称的点为 .
.
(ⅰ)证明: 三点共线;
三点共线;
(ⅱ)求 的面积
的面积 的最大值.
的最大值.
函数 ,给出以下命题:
,给出以下命题:
①函数 有
有 个零点;
个零点;
②若 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 ;
;
③函数 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④
 ,对一切
,对一切 恒成立;
恒成立;
⑤任取 ,
, ,都有
,都有 恒成立.
恒成立.
其中真命题的有
双曲线 的两个焦点为
的两个焦点为 ,若
,若 是双曲线上一点,且
是双曲线上一点,且 ,则双曲线离心率的取值范围为 .
,则双曲线离心率的取值范围为 .
三棱锥 中,
中, 平面
平面 ,
, ,则该三棱锥外接球的体积为 .
,则该三棱锥外接球的体积为 .