已知数列 的前n项和为
的前n项和为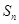 ,且满足
,且满足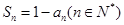 各项为正数的数列
各项为正数的数列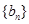 中,对一切
中,对一切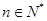 ,有
,有 ,且
,且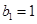 ,
,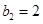 ,
,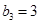 .
.
(1)求数列 和
和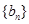 的通项公式.
的通项公式.
(2)设数列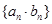 的前n项和为
的前n项和为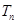 ,求
,求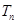 .
.
某投资公司年初用 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出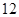 万元,第二年需要支出
万元,第二年需要支出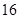 万元,第三年需要支出
万元,第三年需要支出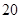 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出 万元,而每年的生产收入都为
万元,而每年的生产收入都为 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用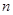 年,
年,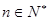 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这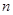 年生产产品相关的各种配套费用的和,生产总利润
年生产产品相关的各种配套费用的和,生产总利润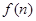 等于这
等于这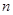 年的生产收入与生产成本的差. 请你根据这些信息解决下列问题:
年的生产收入与生产成本的差. 请你根据这些信息解决下列问题:
(Ⅰ)若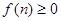 ,求
,求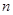 的值;
的值;
(Ⅱ)若干年后,该投资公司对这套生产设备有两个处理方案:
方案一:当年平均生产利润取得最大值时,以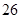 万元的价格出售该套设备;
万元的价格出售该套设备;
方案二:当生产总利润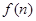 取得最大值时,以
取得最大值时,以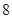 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
已知 .
.
(Ⅰ)写出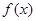 的最小正周期
的最小正周期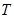 ;
;
(Ⅱ)若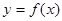 的图象关于直线
的图象关于直线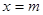 对称,并且
对称,并且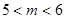 ,求
,求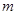 的值.
的值.
已知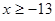 ,关于
,关于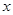 的不等式
的不等式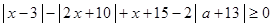 的解集不是空集,求实数
的解集不是空集,求实数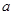 的取值范围.
的取值范围.
已知曲线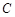 的参数方程为
的参数方程为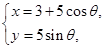
 是参数
是参数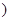 ,
, 是曲线
是曲线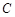 与
与 轴正半轴的交点.以坐标原点
轴正半轴的交点.以坐标原点 为极点,
为极点,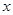 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 与曲线
与曲线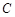 只有一个公共点的直线
只有一个公共点的直线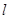 的极坐标方程.
的极坐标方程.
如图,四边形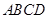 的外接圆为⊙
的外接圆为⊙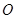 ,
, 是⊙
是⊙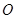 的切线,
的切线,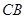 的延长线与
的延长线与 相交于点
相交于点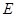 ,
, .
.
求证: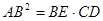 .
.