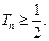(本题共12分,第Ⅰ问4分,第Ⅱ问8分)
设椭圆 过点
过点 ,且左焦点为
,且左焦点为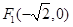 .
.
(Ⅰ)求椭圆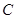 的方程;
的方程;
(Ⅱ)当过点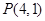 的动直线
的动直线 与椭圆
与椭圆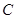 相交于不同两点
相交于不同两点 时,在线段
时,在线段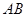 上取点
上取点 ,满足
,满足 .证明:点
.证明:点 总在某定直线上.
总在某定直线上.
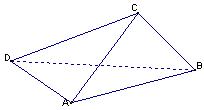
(本小题满分12分)已知矩形ABCD中,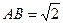 ,
,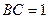 ,现沿对角线
,现沿对角线 折成二面角
折成二面角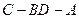 ,使
,使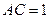 (如图).
(如图).
(I)求证: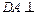 面
面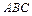 ;
;
(II)求二面角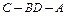 平面角的大小.
平面角的大小.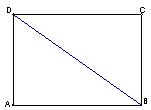
甲、乙、丙三台机床各自独立的加工同一种零件,已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8,乙、丙两台机床加工的零件数相等,甲机床加工的零件数是乙机床加工的零件数的二倍.
(1)从甲、乙、 丙加工的零件中各取一件检验,求至少有一件一等品的概率;
丙加工的零件中各取一件检验,求至少有一件一等品的概率;
(2)将三台机床加工的零件混合到一起,从中任意的抽取一件检验,求它是一等品的概率;
(3)将三台机床加工的零件混合到一起,从中任意的抽取4件检验,其中一等品的个数记为X,求EX.
(本小题满分12分)
设函数
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知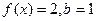 ,△ABC的面积为
,△ABC的面积为 的值。
的值。
设函数 .
.
(Ⅰ)当 曲线
曲线 处的切线斜率;
处的切线斜率;
(Ⅱ)求函数的单调区间与极值
(Ⅲ)已知方程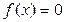 有三个互不相同的实根0,
有三个互不相同的实根0, ,且
,且 .若对任意的
.若对任意的 ,
, 恒成立,求m的取值范围
恒成立,求m的取值范围
等比数列{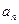 }的前n项和为
}的前n项和为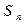 ,已知对任意的
,已知对任意的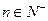 ,点
,点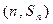 均在函数
均在函数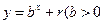 且
且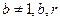 均为常数)的图像上.
均为常数)的图像上.
(Ⅰ)求r的值
(Ⅱ)当b=2时,记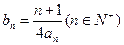 ,数列
,数列 的前n项和
的前n项和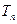 ,求证:
,求证: