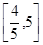在同一平面直角坐标系中,将曲线y= cos2x按伸缩变换
cos2x按伸缩变换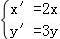 变换为( )
变换为( )
| A.y′=cosx′ | B.y′=3cos ′ ′ |
C.y′=2cos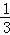 x′ x′ |
D.y′= cos3x′ cos3x′ |
如图所示,已知⊙O的半径为5,两弦AB、CD相交于AB的中点E,且AB=8,CE∶ED=4∶9,则圆心到弦CD的距离为( ).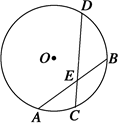
A.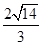 B.
B.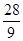 C.
C.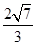 D.
D.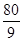
已知随机变量X服从正态分布N(3,1),且 =0.6826,则
=0.6826,则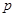 (X>4)=()
(X>4)=()
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.1585 |
已知函数f(x)=bx+1为关于x的一次函数,b为不等0且不等于1的常数,若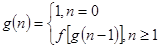 .设
.设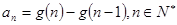 ,则数列
,则数列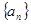 为( )
为( )
A.等差数列 B.等比数列 C递增数列. D.递减数列
设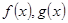 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当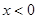 时,
时,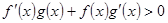 ,且
,且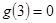 ,则不等式
,则不等式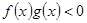 的解集为( )
的解集为( )
A.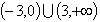 |
B.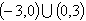 |
C.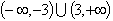 |
D.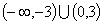 |
已知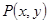 的坐标满足:
的坐标满足: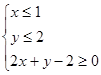 ,那么
,那么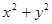 的取值范围是( )
的取值范围是( )
A.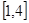 B.
B.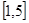 C
C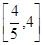 . D.
. D.