选修4﹣2：矩阵与变换
已知二阶矩阵M有特征值λ=3及对应的一个特征向量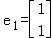
，并且M对应的变换将点（﹣1，2）变换成（9，15），求矩阵M．
已知直线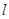
经过抛物线
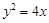的焦点F，且与抛物线相交于A、B两点.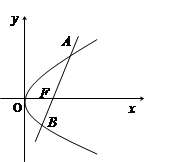
（1）若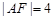
，求点A的坐标；
（2）若直线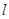的倾斜角为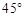
，求线段AB的长.
在正三棱柱ABC-A1B1C1中，若BB1=1，AB=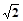
，求AB1与C1B所成角的大小。
已知椭圆的两焦点是F1(0，-1)，F2(0,1)，离心率e=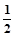
(1)求椭圆方程；(2)若P在椭圆上，且|PF1|-|PF2|=1，求cos∠F1PF2。
已知函数f（x）＝（1＋x）2－4a lnx（a∈N﹡）．
（Ⅰ）若函数f（x）在（1，＋∞）上是增函数，求a的值；
（Ⅱ）在（Ⅰ）的条件下，若关于x的方程f（x）＝x2－x＋b在区间[1，e]上恰有一个实根，求实数b的取值范围．
已知点列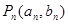
在直线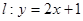
上，P1为直线
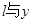轴的交点，等差数列
的公差为1 
。
（1）求、
的通项公式；；
（2）若
，试证数列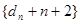
为等比数列，并求
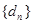的通项公式。
（3）
．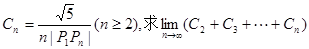