设矩阵A= ,矩阵A属于特征值λ1=﹣1的一个特征向量为α1=
,矩阵A属于特征值λ1=﹣1的一个特征向量为α1= ,属于特征值λ2=4的一个特征向量为α2=
,属于特征值λ2=4的一个特征向量为α2= ,求ad﹣bc的值.
,求ad﹣bc的值.
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 .已知
.已知 .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求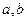 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.

已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为
的离心率为e,右顶点为A,左、右焦点分别为 、
、 ,点E为右准线上的动点,
,点E为右准线上的动点, 的最大值为
的最大值为 .
.
(1)若双曲线的左焦点为 ,一条渐近线的方程为
,一条渐近线的方程为 ,求双曲线的方程;
,求双曲线的方程;
(2)求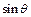 (用
(用 表示);
表示);
(3)如图,如果直线l与双曲线的交点为P、Q,与两条渐近线的交点为 、
、 ,O为坐标原点,求证:
,O为坐标原点,求证:
已知函数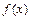 在其定义域上满足
在其定义域上满足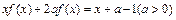 .
.
(1)函数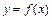 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
(2)当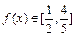 时,求x的取值范围;
时,求x的取值范围;
(3)若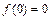 ,数列
,数列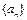 满足
满足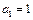 ,那么:
,那么:
①若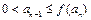 ,正整数N满足
,正整数N满足 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列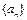 ,
,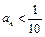 恒成立,求最小的N;
恒成立,求最小的N;
②若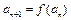 ,求证:
,求证: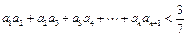 .
.
(本小题满分12分)
设函数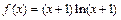 .
.
(1)求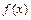 的单调区间
的单调区间
(2)若对所有的 ,均有
,均有 成立,求实数
成立,求实数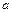 的取值范围.
的取值范围.
(本小题满分12分)
在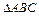 中,
中,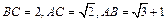 .
.
(1)求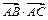 的值;
的值;
(2)若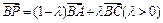 ,且
,且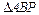 的面积为
的面积为 ,求实数
,求实数 的值.
的值.

