已知函数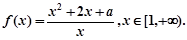
(1)当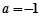 时,判断并证明函数的单调性并求
时,判断并证明函数的单调性并求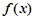 的最小值;
的最小值;
(2)若对任意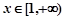 ,
,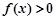 都成立,试求实数
都成立,试求实数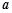 的取值范围.
的取值范围.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ) ,若
,若 ,求a的取值范围.
,求a的取值范围.
(本小题满分12分)已知圆 ,点
,点 ,以线段AB为直径的圆内切于圆
,以线段AB为直径的圆内切于圆 ,记点B的轨迹为
,记点B的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)直线AB交圆 于C,D两点,当B为CD中点时,求直线AB的方程.
于C,D两点,当B为CD中点时,求直线AB的方程.
(本小题满分12分)如图,在斜三棱柱 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
(本小题满分12分)
小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
(本小题满分12分)设数列 的前n项和为
的前n项和为 ,满足
,满足 ,且
,且 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若 成等差数列,求证:
成等差数列,求证: 成等差数列.
成等差数列.