已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,椭圆
,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若过点 的直线
的直线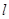 与椭圆
与椭圆 交于不同的两点
交于不同的两点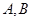 ,且
,且 ,求实数
,求实数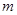 的取值范围.
的取值范围.
已知椭圆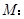
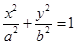 (
( ),点
),点
 、
、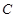
 分别是椭圆
分别是椭圆 的左焦点、左顶点,过点
的左焦点、左顶点,过点 的直线
的直线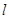 (不与
(不与 轴重合)交
轴重合)交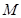 于
于 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若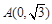 ,求△
,求△ 的面积;
的面积;
(3)是否存在直线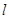 ,使得点
,使得点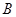 在以线段
在以线段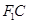 为直径的圆上,若存在,求出直线
为直径的圆上,若存在,求出直线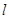 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知函数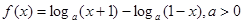 ,且
,且 .
.
(1)求 的定义域;
的定义域;
(2)判断 的奇偶性并予以证明;
的奇偶性并予以证明;
(3)若 时,求使
时,求使 >
> 的
的 的集合.
的集合.
某校为调研学生的身高与运动量之间的关系,从高二男生中随机抽取100名学生的身高数据,得到如下频率分布表:
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
[160,165) |
10 |
0.100 |
| 第2组 |
[165,170) |
① |
0.150 |
| 第3组 |
[170,175) |
30 |
② |
| 第4组 |
[175,180) |
25 |
0.250 |
| 第5组 |
[180,185) |
20 |
0.200 |
| 合计 |
100 |
1.00 |
(1)求频率分布表中①、②位置相应的数据;
(2)为了对比研究学生运动量与身高的关系,学校计划采用分层抽样的方法从第2、5组中随机抽取7名学生进行跟踪调研,求第2、5组每组抽取的学生数?
(3)在(2)的前提下,学校决定从这7名学生中随机抽取2名学生接受调研访谈,求至少有1名学生来自第5组的概率?
如图,已知多面体 中,平面
中,平面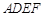 ⊥平面
⊥平面 ,若四边形
,若四边形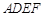 为矩形,
为矩形,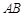 ∥
∥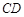 ,
,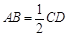 ,
,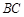 ⊥
⊥ ,
, 为
为 中点.
中点.
(1)求证: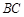 ⊥平面
⊥平面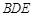 ;
;
(2)求证: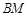 //平面
//平面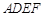 .
.
如图,在平面直角坐标系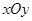 中,以
中,以 轴为始边作角
轴为始边作角 和
和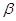 ,
,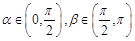 ,其终边分别交单位圆于
,其终边分别交单位圆于 两点.若
两点.若 两点的横坐标分别是
两点的横坐标分别是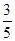 ,
,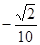 .试求
.试求
(1) ,
, 的值;
的值;
(2) 的值.
的值.