用数学归纳法证明1+2+3+…+(3n+1)= ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
| A.(3k+2) |
| B.(3k+4) |
| C.(3k+2)+(3k+3) |
| D.(3k+2)+(3k+3)+(3k+4) |
在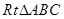 中,
中, 、
、 分别是斜边
分别是斜边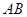 上的高和中线,是该图中共有
上的高和中线,是该图中共有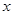 个三角形与
个三角形与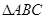 相似,则
相似,则 ( )
( )
A.0 B.1 C.2 D.3
如图4所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC =( )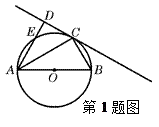
A.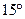 B.
B.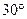 C.
C.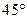 D.
D.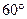
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3。设各车主购买保险相互独立.
(Ⅰ)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(Ⅱ)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
设等比数列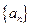 的前n项和为
的前n项和为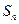 ,已知
,已知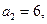
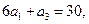 求
求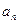 和
和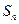 .
.
已知 、
、 分别为双曲线
分别为双曲线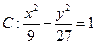 的左、右焦点,点
的左、右焦点,点 ,点M的坐标为
,点M的坐标为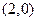 ,AM为∠F1AF2的平分线.则|A
,AM为∠F1AF2的平分线.则|A F2| =.
F2| =.