用数学归纳法证明：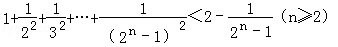
（n∈N*）时第一步需要证明（ ）
A． |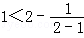
B． |
C． |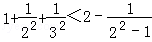
D． |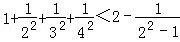
使不等式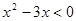
成立的充分不必要条件是（）
| A．0<x<4 | B．0< x < 2 | C．0<x<3 | D．x<0或x>3 |
已知命题p:所有有理数都是实数，命题q:正数的对数都是负数，则下列命题中为真命题的是（ ）
A．（ |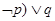
B． |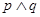
C． |
D． |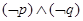
下列函数中，既是偶函数，又在区间（0，+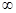
）上单调递减的函数是（）
A．y=x |
B．y=2 |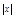
C．y=- |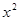
D．y=cosx |
设集合U="{1" ,2 ,3 ,4}，M="{1" ,2 ,3},N={2,3,4},则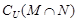
=（）
| A．{1,2} | B．{2，3} | C．{2,4} | D．{1,4} |
对于不等式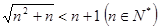
某同学应用数学归纳法证明的过程如下：
（1）当
时，
，不等式成立
（2）假设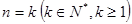
时，不等式成立，即
那么
时，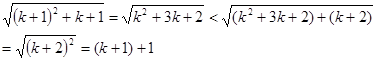
不等式成立根据（1）（2）可知，对于一切正整数
不等式都成立。上述证明方法（）
| A．过程全部正确 | B．验证不正确 |
| C．归纳假设不正确 | D．从 到的推理不正确 |