(15分)右下图为一示波管中的水平偏转极板,已知极板的长度为L,两板距离为d,所加偏转电压为U,且下板带正电;若一束电子以初速 沿极板的中线进入偏转电场,最终电子从P点飞出。设电子的质量为m,电量为e,不计电子的重力。试求
沿极板的中线进入偏转电场,最终电子从P点飞出。设电子的质量为m,电量为e,不计电子的重力。试求
(1)电子在极板间运动的加速度大小;
(2)电子通过极板发生的偏转距离y
(3)若规定图中的上极板电势为零,试求P点的电势。
如图,有两个小朋友玩滑板游戏。起初,甲、乙两个小朋友各坐一辆滑板车在摩擦不计的水平面上相向运动,已知甲连同滑板车的总质量M=30kg,乙连同滑板车的总质量也是M=30kg,甲还推着一只质量m=15kg的放滑板的箱子.甲、乙滑行的速度大小均为2m/s,为了避免相撞,在某时刻甲将箱子沿水平面推给乙,历时0.2秒,箱子滑到乙处时被乙接住.试求
⑴最终甲以多大的速度推出箱子,才可避免和乙相撞?
⑵甲推出箱子时对箱子的冲量多大?
如图所示,直角玻璃三棱镜置于空气中,已知∠A=600, ∠C= 900;一束极细的光于 AC边的中点垂直AC面入射,AC =2a,棱镜的折射率为n= 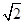 ,求:
,求:
(1)光在棱镜内经一次全反射后第一次射入空气时的折射角。
(2)光从进入棱镜到第一次射入空气时所经历的时间(设光在真空中传播速度为c)。
如图所示,一小球从平台上水平抛出,恰好落在临近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8 m,g=10 m/s2,sin 53°=0.8,cos 53°=0.6,则: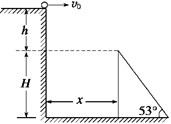
(1)小球水平抛出的初速度v0是多大?
(2)斜面顶端与平台边缘的水平距离x是多少?
(3)若斜面顶端高H=20.8 m,则小球离开平台后经多长时间t到达斜面底端?
两颗卫星在同一轨道平面内绕地球做绕向相同的匀速圆周运动,设地球平均半径为R,a卫星离地面高为R,b卫星离地面高为3R,若某时该两卫星正好同时通过地面同一点正上方,试求从两卫星位于地面同一点正上方开始,两卫星第一次出现最远距离的时间是a卫星周期的几倍?
质量为M长木板放在光滑的水平面上,一个质量为m的滑块以某一速度沿木板表面从A到B点,在木板上前进了L,而木板前进了s,如图,若滑块与木板间的动摩擦因素为μ,则摩擦力对滑块做的功为多少?摩擦力对木板做的功为多少?