气球下挂一重物,以v0=10m/s匀速上升,当到达离地高h=175m处时,悬挂重物的绳子突然断裂,(g取10m/s2)求:
⑴重物离地的最大高度H。
⑵从绳子断裂开始,重物经多少时间落到地面?
⑶重物落地的速度多大?
一个电子在 的电压作用下得到一定速度后垂直于平行板间的匀强电场飞入两板间的中央,如图所示。若平行板间的距离
的电压作用下得到一定速度后垂直于平行板间的匀强电场飞入两板间的中央,如图所示。若平行板间的距离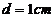 ,板长
,板长 ,问在平行板上加多大电压
,问在平行板上加多大电压 才能使电子刚好飞出平行板?
才能使电子刚好飞出平行板?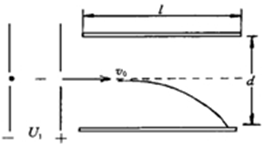
竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该匀强电场中,用丝线悬挂质量为m的带电小球,丝线跟竖直方向成θ角时小球恰好平衡,如图所示.
(1)小球带电荷量是多少?
(2)若剪断丝线,小球碰到金属板需多长时间?
一台电风扇,内阻为20Ω,接上220V电压后,消耗的总功率是66W,求:
(1)电风扇正常工作时通过电动机的电流;
(2)电风扇工作时,转化为机械能和内能的功率
汽车紧急刹车时,加速度大小为9 m/s2,且必须在2 s内停下来。求:
(1)汽车允许的最大行驶速度;
(2)刹车过程汽车最大的位移。
如图所示是做直线运动的物体在0~5s的 图象,求:
图象,求:
(1)0.5s时的速度;
(2)前3s的平均速度;
(3)全程的平均速度;
(4)画出其 图象。
图象。