如图所示,绝缘水平面上的AB区域宽度为d,带正电、电量为q,质量为m的小滑块以大小为v0的初速度从A点进入AB区域,当滑块运动至区域的中点C时,速度大小为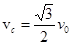 ,从此刻起在AB区域内加上一个水平向左的匀强电场,电场强度E保持不变,并且AB区域外始终不存在电场.
,从此刻起在AB区域内加上一个水平向左的匀强电场,电场强度E保持不变,并且AB区域外始终不存在电场.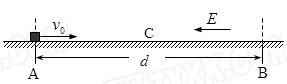
(1)求滑块受到的滑动摩擦力大小.
(2)若加电场后小滑块受到的电场力与滑动摩擦力大小相等,求滑块离开AB区域时的速度.
(3)要使小滑块在AB区域内运动的时间到达最长,电场强度E应满足什么条件?并求这种情况下滑块离开AB区域时的速度.
某学生为了测量一物体的质量,找到了一个力电转换器,该转换器的输出电压正比于受压面的压力(比例系数为k),如图所示。测量时先调节输入端的电压,使转换器空载时的输出电压为0;而后在其受压面上放一物体,即可测得与物体的质量成正比的输出电压U,现有下列器材:力电转换器、质量为m0的砝码、电压表、滑动变阻器、干电池各一个、电键及导线若干、待测物体(可置于力电转换器的受压面上)。请完成对该物体质量的测量。
(1)设计一个电路,要求力电转换器的输入电压可调,并且使电压的调节范围尽可能大,在方框中画出完整的电路图。
(2)简要说明测量步骤,求出比例系数k,并测出待测物体的质量m。
(3)请设想实验中可能出现的一些问题。
人造卫星绕地球运行时,轨道各处地磁场的强弱并不相同,因此,金属外壳的人造地球卫星运行时,外壳中总有微弱的感应电流.分析这一现象中的能量转化情形.它对卫星的运动可能产生怎样的影响?
如图所示:在真空中,有一半径为r的圆形区域内充满垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子质量为m,电量为q,以某一速度由a点沿半径方向射入磁场,从c点射出磁场时其速度方向改变了60度,(粒子的重力可忽略)试求
(1)该粒子在磁场中运动时间t
(2)粒子做圆周运动的半径R
(3)粒子运动的速度
一条长为l、质量为m的均匀链条放在光滑水平桌面上,其中有三分之一悬在桌边,如图所示,在链条的另一端用水平力缓慢地拉动链条,当把链条全部拉到桌面上时,需要做多少功?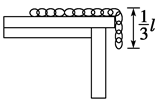
已知质量为m的带电液滴,以速度v射入互相垂直的匀强电场E和匀强磁场B中,液滴在此空间刚好能在竖直平面内做匀速圆周运动,如图所示,求: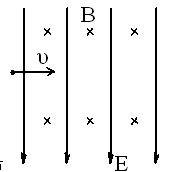
(1)液滴在空间受到几个力作用。
(2)液滴带电荷量及电性。
(3)液滴做匀速圆周运动的半径多大?