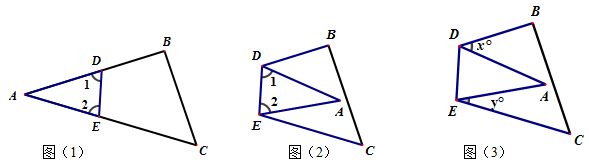
探究：
（1）如图（1），∠1+∠2与∠B+∠C有什么关系？为什么？
（2）把图（2）△ABC沿DE折叠，得到图（2），填空：
∠1+∠2      ∠B+∠C （ 填“＞”“＜”“＝” ），
当∠A=40°时，∠B+∠C+∠1+∠2=           ；
（3）如图（3），是由图（1）的△ABC沿DE折叠得到，若∠A=30°，
则360°-（∠B+∠C+∠1+∠2）=360°-           =        ；
猜想∠BDA+∠CEA与∠A的关系为                               .

科目 数学   题型 解答题   难度 中等

知识点： 三角形的五心