(本题12分)如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE且点A、D、E在同一直线上,连接BE.
(1)若∠ACB="60°," 则∠AEB的度数为 ;
线段AD、BE之间的数量关系是 .
(2)若∠ACB=∠DCE="90°," CM为△DCE中DE边上的高.
①求∠AEB的度数.
②若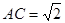 ,
,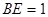 ,试求CM的长.(请写全必要的证明和计算过程)
,试求CM的长.(请写全必要的证明和计算过程)
计算: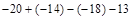
把下列各数分别填入相应的集合里.
1,-0.20, ,325,-789,0,-23.13,0.618,-2004.
,325,-789,0,-23.13,0.618,-2004.
正数集合:{ …};
负数集合:{ …};
分数集合:{…};
整数集合: { …}.
如图所示的图形为四位同学画的数轴,其中正确的是()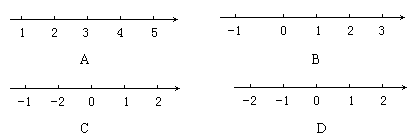
若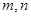 是有理数,求
是有理数,求 的值。
的值。
小红爸爸上星期六买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况。(单位:元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
+4.5 |
-1 |
-2.5 |
-6 |
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了1.5‰的手续费,卖出时还需付成交额,1.5‰的手续费和1‰的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?