(本题6分)我们把分子为1的分数叫做单位分数. 如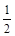 ,
,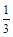 ,
,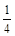 ,任何一个单位分数都可以拆分成两个不同的单位分数的和,如
,任何一个单位分数都可以拆分成两个不同的单位分数的和,如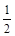 =
=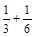 ,
,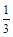 =
=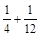 ,
,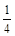 =
=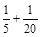 ,
,
 (1)根据对上述式子的观察,你会发现
(1)根据对上述式子的观察,你会发现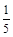 =
=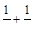 . 请写出□,○所表示的数;
. 请写出□,○所表示的数;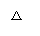
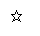 (2)思考,单位分数
(2)思考,单位分数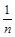 (n是不小于2的正整数)=
(n是不小于2的正整数)=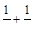 ,请写出△,☆所表示的式.
,请写出△,☆所表示的式.
(3)计算: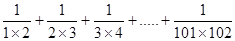
某校对九年级学生进行了一次数学学业水平测试,成绩评定分为A、B、C、D四个等级(注:等级A、B、C、D分别代表优秀、良好、合格、不合格),学校从九年级学生中随机抽取50名学生的数学成绩进行统计分析,并绘制成扇形统计图(如图所示).
根据图中所给的信息回答下列问题: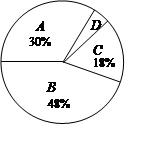
随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?
这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?
若该校九年级学生有800名,请你估计这次数学学业水平测试中,
成绩达合格以上(含合格)的人数大约有多少人?
如图,已知在□ABCD中,延长AB,使AB=BF,连结DF,交BC于点E.求证:E是BC的中点.
先化简,再求值: ,其中
,其中 .
.
计算: .
.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.
求抛物线对应的函数关系式;
若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由
在(2)的条件下,连结BD,已知在对称轴上存在一点P,使得△PBD的周长最小.请求出点P的坐标.
在(2)、(3)的条件下,若点M是线段OB上的一个动点(与点O、B不重合),过点M作MN∥BD交x轴于点N,连结PM、PN,设OM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在最大值?若存在,求出最大值并求此时M点的坐标;若不存在,请说明理由.