（本题12分）如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA=4，OC=2．点P从点O出发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D，点D随点P的运动而运动，连接DP、DA．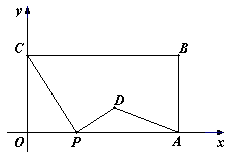
（1）请用含t的代数式表示出点D的坐标；
（2）求t为何值时，△DPA的面积最大，最大为多少？
（3）在点P从O向A运动的过程中，△DPA能否成为直角三角形？若能，求t的值．若不能，请说明理由；
（4）请直接写出随着点P的运动，点D运动路线的长．
（本题12分）如图，在△ABC中，已知AB＝AC，∠BAC＝90o，BC＝6cm，，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒2厘米的速度运动，动点E也同时从点C开始在直线CM上（向上或向下）以每秒1厘米的速度运动，连结AD、AE，设运动时间为t秒．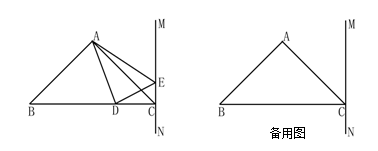
（1）求AB的长；
（2）当t为多少时，△ABD的面积为6cm2？
（3）当t为多少时，△ABD≌△ACE，并简要说明理由（可在备用图中画出具体图形）．
（本题12分）如图，是一个运算流程．
（1）分别计算：当x＝150时，输出值为，当x＝27时，输出值为；
（2）若需要经过两次运算，才能运算出y，求x的取值范围；
（3）请给出一个x的值，使之无论运算多少次都不能输出，并请说明理由．
（本题10分）如图甲，已知：在△ABC中，∠BAC＝90º，AB＝AC，直线m经过点A，BD⊥直线m， CE⊥直线m，垂足分别为点D、E，设BD＝m，CE＝n．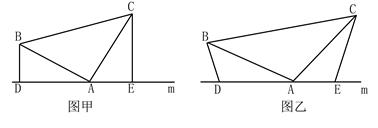
（1）求DE的长（用含m，n的代数式表示）；
（2）如图乙，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝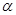
（0º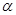＜＜180º），设BD＝m，CE＝n．问DE的长如何表示？并请证明你的结论
（本题10分）如图，在△ABC中，AB＝AC，AD是BC边上的高，AM是△ABC外角∠CAE的平分线．
（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）
（2）设DN与AM交于点F，判断△ADF的形状，并证明你的结论．
某礼品制造工厂接受一批玩具熊的订货任务，按计划天数生产，如果每天生产20个玩具熊，则比订货任务少100个；如果每天生产23个玩具熊，则可以超过订货任务20个．
请求出这批玩具熊的订货任务是多少个？原计划几天完成任务？