题文天气预报说, 在今后的三天中, 每三天下雨的情况不完全相间, 每一天下雨的概率均为40%．现采
用随机模拟试验的方法估计这三天中恰有两天下雨的概率: 用1, 2, 3, 4表示下雨, 从下列随机数表的第1行
第2列开始读取直到末尾从而获得N个数据.据此估计, 这三天中恰有两天下雨的概率近似为 （ ）
19 07 96 61 91  92 52 71 93 28  12 45 85 69 19 16
83 43 12 57 39  30 27 55 64 88  73 01 13 53 79 89

A．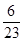

B．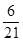

C．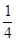

D．非ABC的结果

科目 数学   题型 选择题   难度 较易