如图所示，BCDG是光滑绝缘的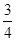
圆形轨道，位于竖直平面内，轨道半径为R，下端与水平绝缘轨道在B点平滑连接，整个轨道处在水平向左的匀强电场中．现有一质量为m、带正电的小滑块(可视为质点)置于水平轨道上，滑块受到的电场力大小为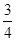mg，滑块与水平轨道间的动摩擦因数μ＝0.5，重力加速度为g.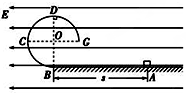
(1)若滑块从水平轨道上距离B点s＝3R的A点由静止释放，滑块到达与圆心O等高的C点时速度为多大？
(2)在(1)的情况下，求滑块到达C点时受到轨道的作用力大小；
(3)改变s的大小，使滑块恰好始终沿轨道滑行，且从G点飞出轨道，求滑块在圆轨道上滑行过程中的最小速度大小．
杆长为L，球的质量为m，杆连球在竖直平面内绕轴O自由转动，已知在最高点处，杆对球的弹力大小为F=1/2mg，求这时小球的即时速度大小。
小球在半径为R的光滑半球内做水平面内的匀速圆周运动，试分析图中的θ（小球与半球球心连线跟竖直方向的夹角）与线速度v、周期T的关系。（小球的半径远小于R。）
固定光滑细杆与地面成一定倾角，在杆上套有一个光滑小环，小环在沿杆方向的推力
作用下向上运动，推力
与小环速度
随时间变化规律如图所示，取重力加速度
．求：
（1）小环的质量
；
（2）细杆与地面间的倾角 ．
如图所示，木槽A质量为
，置于水平桌面上，木槽上底面光滑，下底面与桌面间的动摩擦因数为
，槽内放有两个滑块B和C（两滑块都看作质点），B、C的质量分别
，现用这两个滑块将很短的轻质弹簧压紧（两滑块与弹簧均不连接，弹簧长度忽略不计），此时B到木槽左端、C到木槽右端的距离均为L，弹簧的弹性势能为
。现同时释放B、C两滑块，并假定滑块与木槽的竖直内壁碰撞后不再分离，且碰撞时间极短，求：
（1）B、C与弹簧分离后，B、C的速度
（2）滑块B与槽壁第一次碰撞后的共同速度v1和滑块C与槽壁第二次碰撞后的共同速度v2；
（3）整个运动过程中，木槽与桌面因摩擦产生的热量Q
在光滑水平面上有一质量m＝1.0×10
kg、电量q＝1.0×10
C的带正电小球，静止在O点。以O点为原点，在该水平面内建立直角坐标系Oxy。现突然加一沿X轴正方向、场强大小E＝2.0×106V／m的匀强电场，使小球开始运动。经过1.0s，所加电场突然变为沿y轴正方向，场强大小仍为E＝2.0×106V／m的匀强电场。再经过1.0s，所加电场又突然变为另一个匀强电场，使小球在此电场作用下经1.0s速度变为零。求此电场的方向及速度变为零时小球的位置。