如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB为( )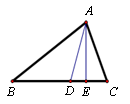
| A.80° | B.72° | C.48° | D.36° |
通过平移把点A(1,-3)移到点A1(3,0),按同样的方式平移直线y=-2x-3得到y=kx+b,则k,b的值分别为
| A.k=-2,b=-4 | B.k=2,b=2 | C.k=-2,b=-2 | D.k="-2,b=4" |
一种商品按进价的100﹪加价后出售,经过一段时间,商家为了尽快减少库存,决定5折销售,这时每件商品
| A.赚50﹪ | B.赔50﹪ | C.赔25﹪ | D.不赔不赚 |
函数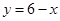 与函数
与函数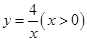 的图象交于A、B两点,设点A的坐标为
的图象交于A、B两点,设点A的坐标为 ,则边长分别为
,则边长分别为 、
、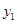 的矩形面积和周长分别为
的矩形面积和周长分别为
A. 4,6
B. 4,12
C. 8,12
D. 8,6
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=2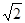 ,AB=
,AB= ,那么sin∠ACD的值是
,那么sin∠ACD的值是
A.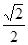 |
B.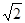 |
C. |
D. |
棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积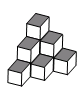
| A.36cm2 | B.33cm2 |
| C.30cm2 | D.27cm2 |