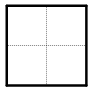
（本题共6分）将一张正方形纸片剪成四个大小、形状一样的小正方-优题课

（本题共6分）将一张正方形纸片剪成四个大小、形状一样的小正方形（如右下图所示），记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：

（1）如果剪100次，共能得到__________个正方形．
（2）如果剪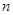次共能得到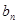个正方形，试用含有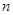、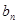的等式表示它们之间的数量关系．
______________________________
（3）若原正方形的边长为1，设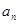表示第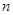次所剪的正方形的边长，
①试用含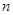的式子表示= ．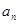
②试猜想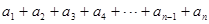与原正方形边长的数量关系，并用等式写出这个关系：__________________________________________．

科目数学题型解答题难度中等

知识点：整式的加减

某商场计划购进 $A$ ， $B$ 两种型号的手机，已知每部 $A$ 型号手机的进价比每部 $B$ 型号手机进价多500元，每部 $A$ 型号手机的售价是2500元，每部 $B$ 型号手机的售价是2100元．商场用50000元共购进 $A$ 型号手机10部， $B$ 型号手机20部．

（1）求 $A$ 、 $B$ 两种型号的手机每部进价各是多少元？

（2）为了满足市场需求，商场决定用不超过7.5万元采购 $A$ 、 $B$ 两种型号的手机共40部，且 $A$ 型号手机的数量不少于 $B$ 型号手机数量的2倍．

①该商场有哪几种进货方式？

②该商场选择哪种进货方式，获得的利润最大？

如图是某路灯在铅垂面内的示意图，灯柱 $AC$ 的高为11米，灯杆 $AB$ 与灯柱 $AC$ 的夹角 $∠ A = 120 °$ ，路灯采用锥形灯罩，在地面上的照射区域 $DE$ 长为18米，从 $D$ ， $E$ 两处测得路灯 $B$ 的仰角分别为 $α$ 和 $β$ ，且 $\tan α = 6$ ， $\tan β = \frac{3}{4}$ ，求灯杆 $AB$ 的长度．

为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成频数分布表如下（成绩得分均为整数） $:$

组别	成绩分组	频数	频率
1	$47.5 ~ 59.5$	2	0.05
2	$59.5 ~ 71.5$	4	0.10
3	$71.5 ~ 83.5$	$a$	0.2
4	$83.5 ~ 95.5$	10	0.25
5	$95.5 ~ 107.5$	$b$	$c$
6	$107.5 ~ 120$	6	0.15
合计		40	1.00

根据表中提供的信息解答下列问题：

（1）频数分布表中的 $a =$ 　　， $b =$ 　　， $c =$ 　　；

（2）已知全区八年级共有200个班（平均每班40人），用这份试卷检测，108分及以上为优秀，预计优秀的人数约为　　，72分及以上为及格，预计及格的人数约为　　，及格的百分比约为　　；

（3）补充完整频数分布直方图．

如图，已知四边形 $ABCD$ 是平行四边形，点 $E$ ， $F$ 分别是 $AB$ ， $BC$ 上的点， $AE = CF$ ，并且 $∠ AED = ∠ CFD$ ．

求证：（1） $ΔAED ≅ ΔCFD$ ；

（2）四边形 $ABCD$ 是菱形．

如图，抛物线顶点 $P (1, 4)$ ，与 $y$ 轴交于点 $C (0, 3)$ ，与 $x$ 轴交于点 $A$ ， $B$ ．

（1）求抛物线的解析式．

（2） $Q$ 是抛物线上除点 $P$ 外一点， $ΔBCQ$ 与 $ΔBCP$ 的面积相等，求点 $Q$ 的坐标．

（3）若 $M$ ， $N$ 为抛物线上两个动点，分别过点 $M$ ， $N$ 作直线 $BC$ 的垂线段，垂足分别为 $D$ ， $E$ ．是否存在点 $M$ ， $N$ 使四边形 $MNED$ 为正方形？如果存在，求正方形 $MNED$ 的边长；如果不存在，请说明理由．