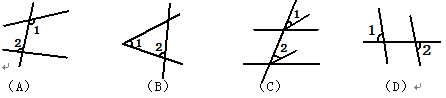把代数式“
”用文字语言叙述，其中表述不正确的是（ ）
| A．比x的倒数小5的数 | B．x的倒数与5的差 |
| C．x与5的差的倒数 | D．1除以x的商与5的差 |
八年级（１）班５０名学生的年龄统计结果如下表所示：则此班学生年龄的众数、中位数分别为……………………………………………………………（ ▲ ）
| 年龄 |
13 |
14 |
15 |
16 |
| 人数 |
4 |
22 |
23 |
1 |
A．14，14 B．15，14 C．14，15 D．15，16
下列图形中，不是轴对称图形的是……………………………（ ▲ ）
| A．线段 | B．角 | C．等腰三角形 | D．直角三角形 |
下列调查方式合适的是………………………………………（ ▲ ）
| A．为了解人们保护水资源的意识,采用抽样调查的方式 |
| B．为了解全国中学生的眼睛视力状况,采用普查的方式 |
| C．为了解炮弹的杀伤力,采用普查的方式 |
| D．对探月航天器“嫦娥2号”零部件的检查,采用抽样调查的方式 |
下列几何体不属于多面体的是……………………………（ ▲ ）
| A．三棱锥 | B．球体 | C．立方体 | D．四面体 |
如图，∠1和∠2是同位角的是 ………………………（ ▲）