李老师从“淋浴龙头”受到启发.编了一个题目:
在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当 时,求n的值.你解答这个题目得到的n值为( )
时,求n的值.你解答这个题目得到的n值为( )
A. |
B. |
C. |
D. |
如图所示,数轴上在﹣2和﹣1之间的长度以小隔线分成八等分,A点在其中一隔,则A点表示的数是( )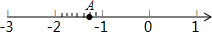
A.﹣1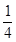 |
B.﹣1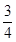 |
C.﹣2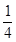 |
D.﹣2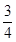 |
如图,数轴上A、B两点对应的实数分别为a,b,则下列结论不正确的是( )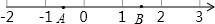
A.a+b>0 B.ab<0 C.a﹣b<0 D.|a|﹣|b|>0
如图,数轴上A、B两点对应的实数分别是1和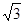 ,若点A关于点B的对称点为点C,则点C所对应的实数为( )
,若点A关于点B的对称点为点C,则点C所对应的实数为( )
A.2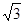 ﹣1 B.1+
﹣1 B.1+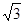 C.2+
C.2+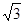 D.2
D.2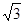 +1
+1
如图所示,数轴上两点A,B分别表示实数a,b,则下列四个数中最大的一个数是( )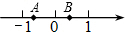
| A.a | B.b | C.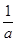 |
D.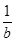 |
如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( )
| A.|a|>|b| | B.a+b>0 | C.ab<0 | D.|b|=b |