在下图中,每个正方形由边长为1 的小正方形组成:
| 正方形边长 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
| 黑色小正方形个数 |
1 |
4 |
5 |
8 |
|
|
|
|
|
(1)观察图形,请填写下列表格;
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1,白色小正方形的个数
为P2,问是否存在偶数n,使P2="5" P1?若存在,请求出n的值;若不存在,请说明理由.
如图,在 中, ,以 的边 为直径作 ,交 于点 ,过点 作 ,垂足为点 .
(1)试证明 是 的切线;
(2)若 的半径为5, ,求此时 的长.

如图,已知反比例函数 的图象与直线 相交于点 , .
(1)求出直线 的表达式;
(2)在 轴上有一点 使得 的面积为18,求出点 的坐标.

如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼 的高度进行测量,先测得居民楼 与 之间的距离 为 ,后站在 点处测得居民楼 的顶端 的仰角为 ,居民楼 的顶端 的仰角为 ,已知居民楼 的高度为 ,小莹的观测点 距地面 .求居民楼 的高度(精确到 .(参考数据: , , .

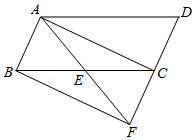
如图,在 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 , ,若 ,求证:四边形 是矩形.
今年植树节期间,某景观园林公司购进一批成捆的 , 两种树苗,每捆 种树苗比每捆 种树苗多10棵,每捆 种树苗和每捆 种树苗的价格分别是630元和600元,而每棵 种树苗和每棵 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵, 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进 种树苗和 种树苗各多少棵?并求出最低费用.