下列命题:①数列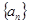 为递减的等差数列且
为递减的等差数列且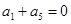 ,设数列
,设数列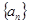 的前
的前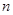 项和为
项和为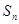 ,则当
,则当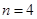 时,
时,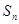 取得最大值;②设函数
取得最大值;②设函数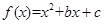 ,则
,则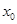 满足关于
满足关于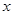 的方程
的方程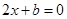 的充要条件是对任意
的充要条件是对任意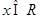 均有
均有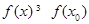 ;③在长方体
;③在长方体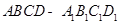 中,
中,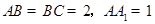 ,直线
,直线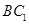 与平面
与平面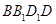 所成角的正弦值为
所成角的正弦值为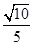 ;④定义在
;④定义在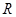 上的函数
上的函数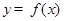 满足
满足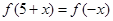 且
且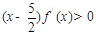 ,已知
,已知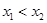 ,则
,则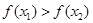 是
是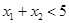 的充要条件.
的充要条件.
其中正确命题的序号是 (把所有正确命题的序号都写上).
2012年伦敦奥运火炬接力在希腊的传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有_________种.(用数字作答).
设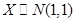 ,则
,则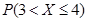 =.
=.
已知两点A(-1,0),B(0,2),点C是圆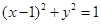 上任意一点,则△ABC面积的最小值是______________.
上任意一点,则△ABC面积的最小值是______________.
过点O(0,0)引圆C: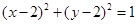 的两条切线OA,OB,A,B为切点,则直线AB的方程是______________.
的两条切线OA,OB,A,B为切点,则直线AB的方程是______________.
如图,在正方体ABCD-A1B1C1D1中,异面直线A1B与AC所成的角是______°;直线A1B和平面A1B1CD所成的角是_________°.