已知关于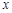 的一元二次方程
的一元二次方程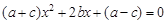 ,其中a、b、c分别为△ABC三边的长.
,其中a、b、c分别为△ABC三边的长.
(1)如果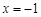 是方程的根,试判断△ABC的形状,并说明理由;
是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(3)如果△ABC是等边三角形,试求这个一元二次方程的根.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延 长交BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
某景点的门票价格如表:
| 购票人数/人 |
1~50 |
51~100 |
100以上 |
| 每人门票价/元 |
12 |
10 |
8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
计算: ﹣
﹣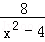 .
.
阅读材料:善于思考的小军在解方程组 时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y="5" 即2(2x+5y)+y=5③
时,采用了一种“整体代换”的解法:将方程②变形:4x+10y+y="5" 即2(2x+5y)+y=5③
把方程①带入③得:2×3+y=5,∴y=﹣1
把y=﹣1代入①得x=4,∴方程组的解为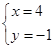 .
.
请你解决以下问题:(1)模仿小军的“整体代换”法解方程组 ;
;
(2)已知x,y满足方程组 .
.
(i)求 的值;
的值;
(ii)求 的值.
的值.
白溪镇2012年有绿地面积57.5公顷,该镇近几年不断增加绿地面积,2014年达到82.8公顷.
(1)求该镇2012至2014年绿地面积的年平均增长率;
(2)若年增长率保持不变,2015年该镇绿地面积能否达到100公顷?