《莱因德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给五个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,问最小1份为( )
是较小的两份之和,问最小1份为( )
A. |
B. |
C. |
D. |
设函数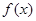 在定义域内可导,
在定义域内可导, 图象如下图所示,则导函数
图象如下图所示,则导函数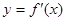 的图象可能为( )
的图象可能为( )
对大于或等于2的自然数的正整数幂运算有如下分解方式:
22=1+3 32=1+3+5 42=1+3+5+7
23=3+5 33=7+9+11 43=13+15+17+19
根据上述分解规律,若 ,
, 的分解中最小的正整数是21,则
的分解中最小的正整数是21,则 ( )
( )
A. |
B.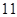 |
C. |
D.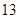 |
若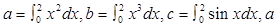 、
、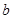 、
、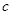 大小关系是()
大小关系是()
A.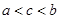 |
B. |
C. |
D.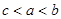 |
我校为了提高学生的英语口语水平,招聘了6名外籍教师,要把他们安排到3个宿舍去住,每个宿舍住2人,其中教师甲必须住在一号宿舍,教师乙和教师丙不能住到三号宿舍,则不同的安排方法数共有()
| A.6 | B.9 | C.12 | D.18 |
某种产品的广告费支出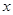 与销售额
与销售额 (单位:万元)之间有如下一组数据:
(单位:万元)之间有如下一组数据:
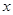 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
若 与
与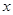 之间的关系符合回归直线方程
之间的关系符合回归直线方程 ,则
,则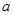 的值是()
的值是()
A.17.5B.27.5 C.17D.14