下面对命题“函数f(x)=x+ 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )
A.∀x∈R且x≠0有f(﹣x)=(﹣x)+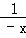 =﹣(x+ =﹣(x+ )=﹣f(x),∴f(x)是奇函数 )=﹣f(x),∴f(x)是奇函数 |
B.∀x∈R且x≠0有f(x)+f(﹣x)=x+ +(﹣x)+(﹣ +(﹣x)+(﹣ )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数 )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数 |
C.∀x∈R且x≠0,∵f(x)≠0,∴ = = =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数 =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数 |
D.取x=﹣1,f(﹣1)=﹣1+ =﹣2,又f(1)=1+ =﹣2,又f(1)=1+ =2 =2 |
已知一个三角形的三边长构成等比数列,其公比为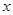 ,则函数
,则函数 =
= -
- 的值域为
的值域为
A.(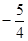 ,+∞) ,+∞) |
B.[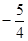 ,+∞) ,+∞) |
C.(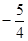 ,-1) ,-1) |
D.[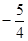 ,-1) ,-1) |
△ABC的内角A、B、C的对边分别为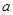 、
、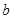 、
、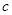 ,若
,若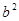 =
=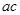 ,且
,且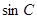 =2
=2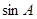 ,则
,则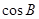 等于()
等于()
A、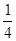 B、
B、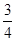 C、
C、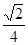 D、
D、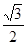
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积之和的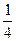 ,且样本容量为160,则中间一组的频数为()
,且样本容量为160,则中间一组的频数为()
| A.32 | B.36 | C.40 | D.42 |
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分 的十位数,据图可知()
的十位数,据图可知()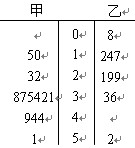
| A.甲运动员的最低得分为0分 |
| B.甲运动员得分的众数为44分 |
| C.乙运动员得分的中位数是29分 |
| D.乙运动员得分的平均值在区间(11、19)内 |
“ab<0”是“曲线ax2+by2=1为双曲线”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |