用反证法证明命题:“a,b,c,d∈R,a+b=1,c+d=1,且ac+bd>1,则a,b,c,d中至少有一个负数”时的假设为( )
| A.a,b,c,d中至少有一个正数 |
| B.a,b,c,d全为正数 |
| C.a,b,c,d全都大于等于0 |
| D.a,b,c,d中至多有一个负数 |
下列判断正确的是 ( )
A.若向量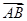 与 与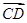 是共线向量,则A,B,C,D四点共线; 是共线向量,则A,B,C,D四点共线; |
| B.单位向量都相等; |
| C.共线的向量,若起点不同,则终点一定不同; |
| D.模为0的向量的方向是不确定的。 |
已知 ,则角
,则角 所在的象限是()
所在的象限是()
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知圆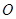 的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么
的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么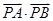 的最小值为( )
的最小值为( )
A. 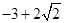 B.
B. C .
C .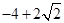 D.
D.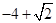
在平面直角坐标系中,若不等式组 (
(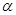 为常数)所表示的平面区域内的面积等于2,则
为常数)所表示的平面区域内的面积等于2,则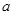 的值为()
的值为()
| A.-5 | B.1 | C.2 | D.3 |
下列四类函数中,有性质“对任意的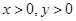 ,函数
,函数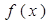 满足
满足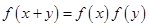 ”是()
”是()
| A.指数函数 | B.对数函数 | C.幂函数 | D.余弦函数 |