用反证法证明命题“设a,b∈R,|a|+|b|<1,a2﹣4b≥0那么x2+ax+b=0的两根的绝对值都小于1”时,应假设( )
| A.方程x2+ax+b=0的两根的绝对值存在一个小于1 |
| B.方程x2+ax+b=0的两根的绝对值至少有一个大于等于1 |
| C.方程x2+ax+b=0没有实数根 |
| D.方程x2+ax+b=0的两根的绝对值都不小于1 |
[2014·江西模拟]已知偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1)<f(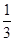 )的x的取值范围是( )
)的x的取值范围是( )
A.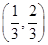 |
B.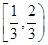 |
C.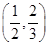 |
D.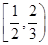 |
[2013·山东高考]已知函数f(x)为奇函数,且当x>0时,f(x)=x2+ ,则f(-1)=( )
,则f(-1)=( )
| A.-2 | B.0 | C.1 | D.2 |
[2013·吉林调研]已知定义在R上的函数f(x)满足f(x)+f(-x)=0,且在(-∞,0)上单调递增,如果x1+x2<0且x1x2<0,则f(x1)+f(x2)的值( )
| A.可能为0 | B.恒大于0 |
| C.恒小于0 | D.可正可负 |
[2014·日照模拟]已知函数f(x)在定义域(0,+∞)上是单调函数,若对于任意x∈(0,+∞),都有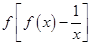 =2,则
=2,则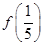 的值是( )
的值是( )
| A.5 | B.6 | C.7 | D.8 |
[2014·大庆质检]下列函数中,满足“对任意的x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
A.f(x)=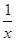 |
B.f(x)=(x-1)2 |
| C.f(x)=ex | D.f(x)=ln(x+1) |