下列命题中，
①命题“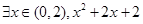
<
” 的否定是“
＞”；
②
是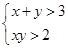
的充要条件；
③一个命题的逆命题为真，它的否命题也一定为真；
④“9＜
＜15”是“方程
表示椭圆”的充要条件．
⑤设
是以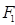
、
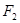为焦点的双曲线一点，且
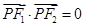，若
的面积为
，则双曲线的虚轴长为6；
其中真命题的是 （将正确命题的序号填上）
若 
＝3＋ln 2(a>1)，则a的值是______．
已知定义在R上的偶函数满足：f(x＋4)＝f(x)＋f(2)，且当x∈[0,2]时，y＝f(x)单调递减，给出以下四个命题：
①f(2)＝0；
②x＝－4为函数y＝f(x)图象的一条对称轴；
③函数y＝f(x)在[8,10]上单调递增；
④若方程f(x)＝m在[－6，－2]上的两根为x1，x2则x1＋x2＝－8.以上命题中所有正确命题的序号为________．
已知定义在R上的函数f(x)的图象关于点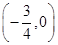
成中心对称，对任意实数x都有f(x)＝－
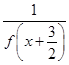，且f(－1)＝1，f(0)＝－2，则f(0)＋f(1)＋…＋f(2013)＝________.
某公司购买一批机器投入生产，据市场分析每台机器生产的产品可获得的总利润y(单位：万元)与机器运转时间x(单位：年)的关系为y＝－x2＋18x－25(x∈N*)．则当每台机器运转______年时，年平均利润最大，最大值是______万元．
定义a*b＝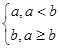
已知a＝30.3，b＝0.33，c＝log30.3，则(a*b)*c＝______(用a，b，c作答)．