已知函数f（x）满足2f（x＋2）＝f（x），当x∈（0，2）时，f（x）＝lnx＋ax （
），当x∈（―4，―2）时，f（x）的最大值为―4．
（1）求x∈（0，2）时，f（x）的解析式；
（2）是否存在实数b使得不等式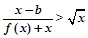
对于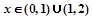
恒成立？若存在，求出实数b的取值集合；若不存在，请说明理由．
已知点
为
轴上的动点，点
为
轴上的动点，点
为定点，且满足
，
.
（Ⅰ）求动点
的轨迹
的方程；
（Ⅱ）过点
且斜率为
的直线
与曲线交于两点
，
，试判断在轴上是否存在点
，使得
成立，请说明理由.
某售报亭每天以每份0.4元的价格从报社购进若干份报纸，然后以每份1元的价格出售，如果当天卖不完，剩下的报纸以每份0.1元的价格卖给废品收购站.
（Ⅰ）若售报亭一天购进270份报纸，求当天的利润
(单位：元)关于当天需求量
（单位：份，
）的函数解析式.
（Ⅱ）售报亭记录了100天报纸的日需求量（单位：份），整理得下表：
| 日需求量 |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
| 频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
以100天记录的需求量的频率作为各销售量发生的概率.
（1）若售报亭一天购进270份报纸，
表示当天的利润（单位：元），求的数学期望；
（2）若售报亭计划每天应购进270份或280份报纸，你认为购进270份报纸好，还是购进280份报纸好? 说明理由.
如图，在四棱锥
中，
平面
，底面
是菱形，
，
．
（Ⅰ）求证：
；
（Ⅱ）若
，求二面角
的余弦值.
在
中，角
、
、
的对边分别为
、
、
，
.
（Ⅰ）求角的大小；
（Ⅱ）若
，
，求的值．
（本小题满分15分）
已知函数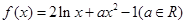
（Ⅰ）求函数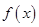
的单调区间；
（Ⅱ）若
，试分别解答以下两小题.
（ⅰ）若不等式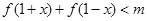
对任意的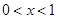
恒成立，求实数
的取值范围；
（ⅱ）若
是两个不相等的正数，且
，求证：
．