(本小题满分14分)设函数 .
.
(1)若函数 在
在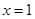 处与直线
处与直线 相切:
相切:
①求实数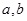 的值;
的值;
②求函数 在
在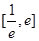 上的最大值;
上的最大值;
(2)当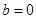 时,若不等式
时,若不等式 ≥
≥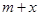 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
如图,在三棱锥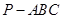 中,
中,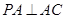 ,
,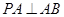 ,
,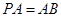 ,
,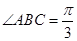 ,
,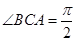 , 点
, 点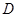 ,
,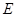 分别在棱
分别在棱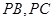 上,且
上,且 ,
,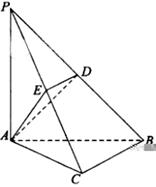
(Ⅰ)求证: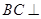 平面PAC
平面PAC
(Ⅱ)当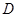 为
为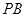 的中点时,求
的中点时,求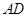 与平面
与平面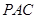 所成的角的正弦值;
所成的角的正弦值;
(Ⅲ)是否存在点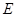 使得二面角
使得二面角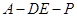 为直二面角?并说明理由.
为直二面角?并说明理由.
等差数列 的各项均为正数,
的各项均为正数,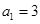 ,前
,前 项和为
项和为 ,
, 为等比数列,
为等比数列,  ,且
,且
 .
.
(1)求 与
与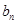 ;
;
(2)求数列 的前
的前 项和
项和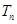 。
。
(本小题满分12分)
在 中,a,b,c分别是角A,B,C的对边,已知
中,a,b,c分别是角A,B,C的对边,已知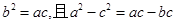
(1)求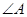 的大小;
的大小;
(2)设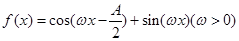 且
且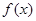 的最小正周期为
的最小正周期为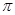 ,求
,求 的最大值。
的最大值。
已知 是实数,函数
是实数,函数 。
。
(Ⅰ)若 ,求
,求 的值及曲线
的值及曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间 上的最大值。
上的最大值。
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?