定义在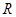 上的奇函数
上的奇函数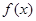 和定义在
和定义在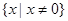 上的偶函数
上的偶函数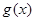 分别满足
分别满足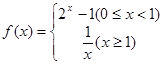 ,
,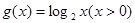 ,若存在实数
,若存在实数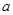 ,使得
,使得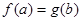 成立,则实数
成立,则实数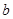 的取值范围是( )
的取值范围是( )
A.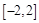 |
B.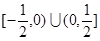 |
C.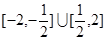 |
D.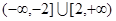 |
下列命题中正确的是()
A. , , 是两个相交的平面, 是两个相交的平面,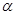 内存在两条相交直线都平行于 内存在两条相交直线都平行于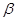 |
| B.两个不同的平面存在三个不共线的公共点 |
| C.经过一直线与一点有唯一一个平面 |
| D.经过平面外一点的直线一定在平面外。 |
 ,
,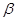 是两个不重合的平面,在下列条件中,可以判断
是两个不重合的平面,在下列条件中,可以判断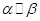 的是()
的是()
A.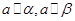 . . |
B. 有三个不共线的点到 有三个不共线的点到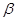 的距离相等 的距离相等 |
C. |
D. 为异面直线且 为异面直线且 |
已知a,b是两条异面直线,直线c a,那么c与b的位置关系是()
a,那么c与b的位置关系是()
| A.一定是异面 | B.一定是相交 | C.不可能平行 | D.可能相交 |
 是空间三条不同的直线,则下列命题正确的是()
是空间三条不同的直线,则下列命题正确的是()
A.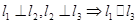 |
B. |
C.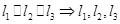 共面 共面 |
D. 共点 共点  共面 共面 |
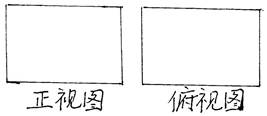
右图是长和宽分别相等的两个矩形。给定下列三个命题:(1)存在三棱柱,其正视图,俯视图如右图;(2)存在四棱柱,其正视图,俯视图如右图;(3)存在圆柱,其正视图,俯视图如右图。其中真命题的个数是()
| A.3 | B.2 | C.1 | D.0 |