如图①,在平面直角坐标系中,直线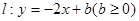 的位置随b的不同取值而变化.
的位置随b的不同取值而变化.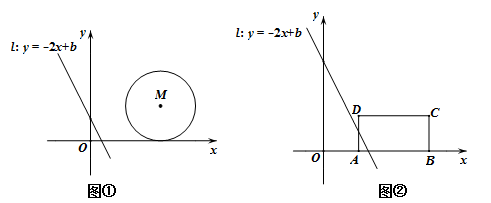
(1)已知⊙M的圆心坐标为(4,2),半径为2,
当b= 时,直线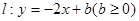 经过圆心M ;
经过圆心M ;
当b= 时,直线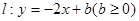 与 ⊙M相切;
与 ⊙M相切;
(2)若把⊙M换成矩形ABCD,如图②,其三个顶点的坐标分别为:A(2,0),B(6,0),C(6,2) .设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.
如图,□ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
(1)求证:△AOE≌△COF.
(2)连接EC、AF,则EF与AC满足什么条件时,四边形AECF是矩形?并说明理由.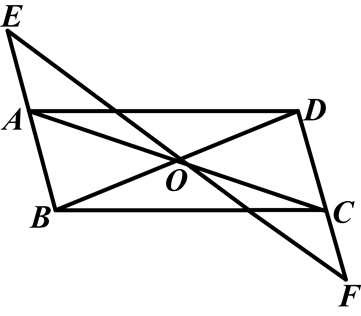
如图,在□ABCD中,E、F分别是边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF.
(2)若∠G=90°,求证:四边形DEBF是菱形.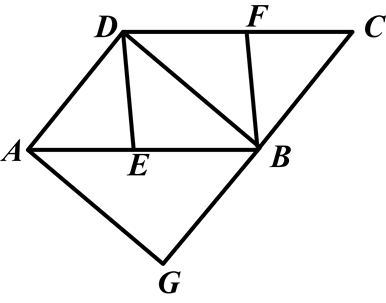
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC.
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.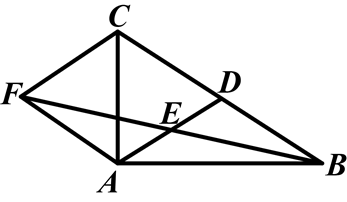
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F.连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,证明:四边形ABCD是菱形.
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
如图,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,CD平分∠ECA.
求证:四边形ABCD是菱形.