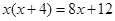某服装柜在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件,现商场决定采取适当的降价措施,扩大销售量,增加盈利,经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种服装盈利l200元,同时又要使顾客得到较多的实惠,那么每件服装应降价多少元?
2011年辽宁卫视举办的“激情唱响”活动风靡全国.比赛中,甲、乙、丙三位评委对选手的综合表现,分别给出“Yes”或“No”的评判结论(其中“Yes”是指“通过”,“No”是指不通过).
(1)请用“树形图法”或“列表法”,求出对于选手A,只有甲、乙两位评委给出相同评判结论的概率是多少?
(2)按照比赛规则,若三位评委中只要有两位给出“Yes”的结论,则参赛选手就可直接获得晋级下一轮比赛的资格,请求出选手A直接获得晋级下一轮比赛资格的概率是多少?
如图6所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.(要求:用直尺作出图形即可,不用保留作图痕迹,不写作法.)
(2) 点B1的坐标是,点C2的坐标是.
(3) 求△ABC绕点A逆时针旋转90°的过程中,线段AB扫过的面积.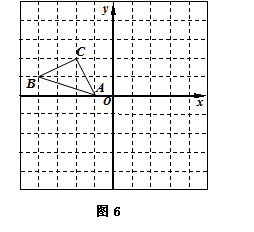
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图5所示的统计图,根据统计图提供的信息解决下面问题:
⑴ 柑橘损坏的概率估计值为,柑橘完好的概率估计值为;
⑵ 估计这批柑橘完好的质量为千克;
⑶ 如果公司希望销售这些柑橘能够获得25000元的利润,那么在出售(已去掉损坏的柑橘)时,每千克柑橘大约定价为多少元比较合适?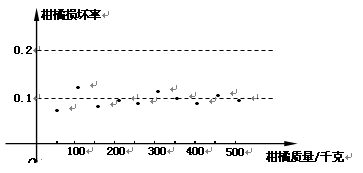
在国家政策的宏观调控下,某市的商品房成交均价由2011年10月底的20000元/m2下降到2011年12月底的16200元/m2.
(1)求2011年11、12两月平均每月降价的百分率是多少?
(2)如果房价继续按此降价的百分率回落,请你预测到2012年2月底该市的商品房成交均价是否会跌破13000元/m2?并说明理由.
解方程: