如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒后,M、N两点 重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
如图,有一块直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
在一次“探究性学习”课中,数学老师给出如下表所示的数据:
请你认真观察线段a、b、c的长与n之间的关系,用含n(n为自然数,且n>1)的代数式
表示: a=b=c=
猜想:以线段a、b、c为边的三角形是否是直角三角形?并说明你的结论.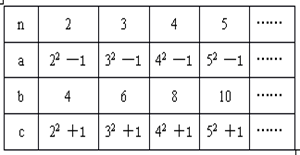
如图, E是长方形ABCD边AD的中点, AD =" 2AB" =" 2" ,求ΔBCE的面积和周长.(结果保留根号)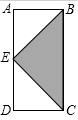
学完勾股定理之后,同学们想利用升旗的绳子、卷尺,测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案:将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米.请你设法帮小明算出旗杆的高度.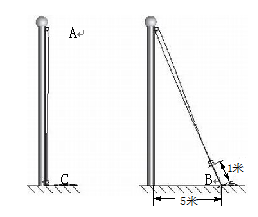
如图,已知每一个小正方形的边长为1,求△ABC的面积.