我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由高到低的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2=a2+2ab+b2展开式中的系数;第四行的四个数1，3，3，1，恰好对应着（a+b）3=a3+3a2b+3ab2+b2展开式中的系数等．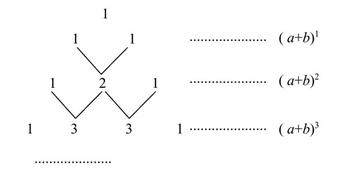
（1）根据上面的规律，写出（a+b）5的展开式．
（2）利用上面的规律计算：
25-5×24+10×23-10×22+5×2-1．
如图，已知△ABC中，AC=10
，AB=16，问在AB边上是否存在这样的点P，使△APC∽△ACB，若存在，求AP的长；若不存在，请说明理由．
、在中国地理地图册上，连接上海，香港，台湾三地构成一个三角形，用刻度迟测得他们之间的距离。上海----香港5. 4cm , 上海-----台湾 3cm , 香港------台湾3. 6cm .飞机从台湾直飞到上海的距离为1286千米，那么飞机从台湾绕道香港再到上海的空中飞行距离是多少千米？
某同学将一张报纸对折后，发现对折后的半张报纸与整张报纸恰好相似，如图所示
求整张报纸的长和宽的比是多少？ 
、如图所示为一矩形木框，四周为宽度相同的木条，那么这个矩形框的里、外两个矩形是相似形吗？假设木框长为30 cm宽为20cm，木条的宽度为2 cm，试加以验证。
证明：任意两个正六边形是相似形