解方程:
随着“十一五”期间中央系列强农惠农政策的出台,农民的收入和生活质量及消费走势发生了巨大的变化,农民的生活消费结构趋于理性化,并呈现出多层次的消费结构,为了解我市农民消费结构状况,随机调查了部分农民,并根据调查数据,将2008年和2010年我是农民生活消费支出情况绘成了如下的统计图表:
请解答如下问题:
(1)2008年的生活消费,支出总额是多少?支出费用中支出最多的项目是哪一项?
(2)2010年我市农民生活消费支出构成表中a、b、c的值分别是多少?
(3)2008年到2010年的生活消费支出总额的年平均增长率是多少?
如图,已知四边形ABCD是平行四边形.
(1)求证:△MEF∽△MBA;
(2)若AF、BE分别是∠DAB,∠CBA的平分线,求证:DF=EC.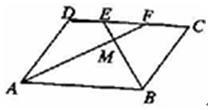
在1个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外,其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白色的概率为0.5.
(1)求口袋中红球的个数;
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球,不放回,再找出一个画树状图的方法求甲摸的两个球且得2分的概率.
先化简,再求值,( +
+ )÷
)÷ ,其中x=2.
,其中x=2.
解不等式组 .
.